剑指 Offer 62. 圆圈中最后剩下的数字

https://leetcode-cn.com/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof/

此问题称作 约瑟夫环 问题。

参考题解：https://leetcode-cn.com/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof/solution/huan-ge-jiao-du-ju-li-jie-jue-yue-se-fu-huan-by-as/

递推公式定义：

f(n, m) 表示环长度为 n，每次杀掉第 m 人，最后生下来的人 在 当前序列 中的 index。由于这个人是活到最后的，所以他在任何子问题 f(n-i, m) 中都是活着的，只不过可能因为其他人被杀掉所以他 index 变了，且在 f(0, m) 中他的序号是 0（唯一活着的人）。

问题就是怎么找出他在不同序列中序号的变化。看图：

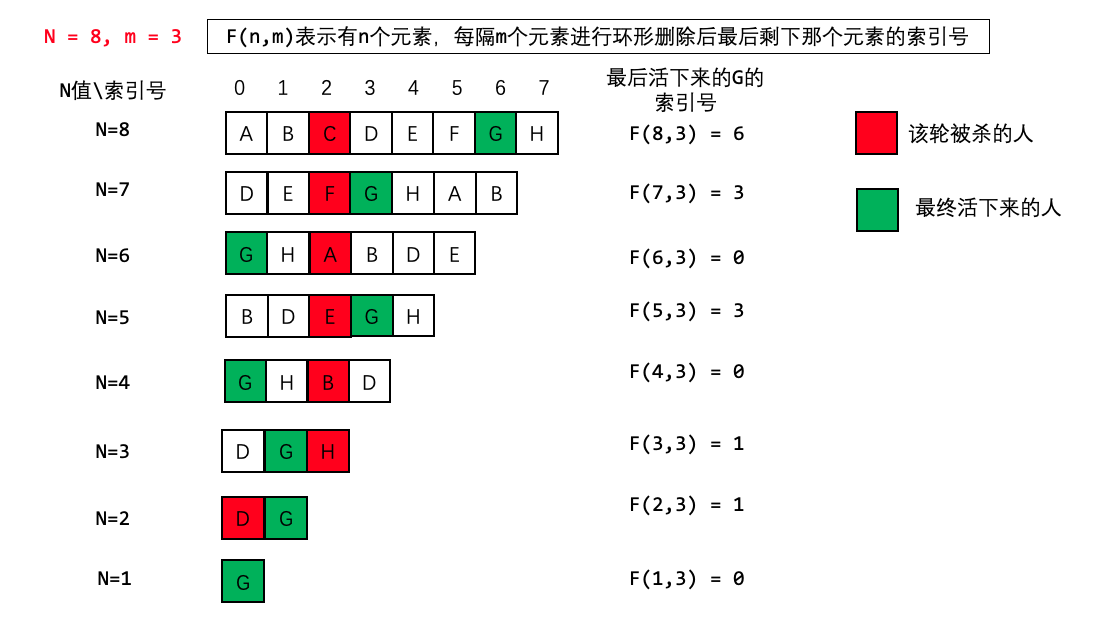
观察 N = 8 和 N = 7 的变化，N = 8 时，这个人的序号是 6，而 N = 7 时变成了 3。

首先考虑怎么将 N = 7 时的序列复原回 N = 8 时的样子。观察发现，将被杀掉 C 加回末尾，然后令数组顺时针旋转 3 格，就得到了原来的序列。如何表示这个变化呢？看图：

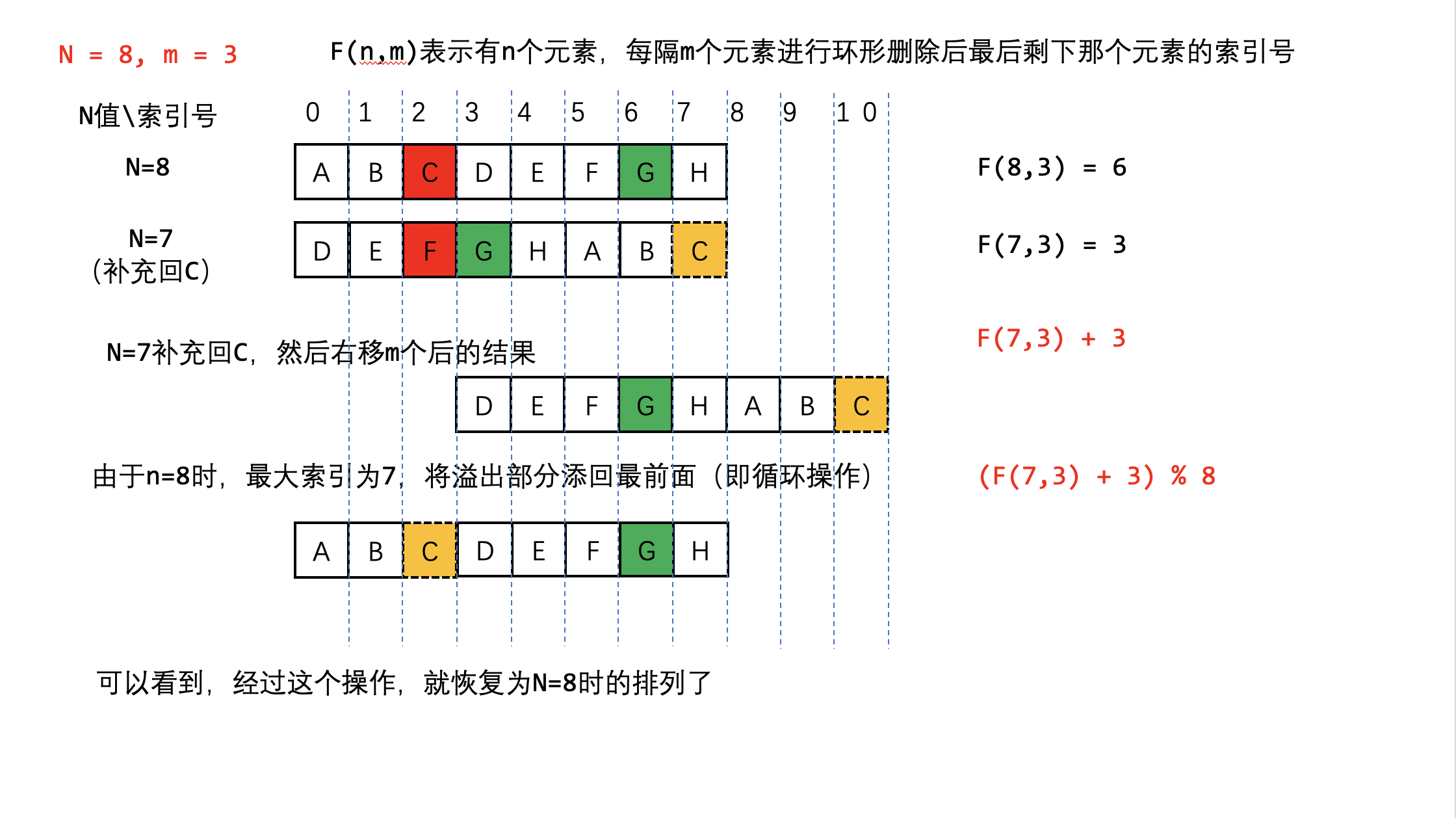
至此，递归公式已被找出，可以直接从 0 开始推起。

func lastRemaining(n int, m int) int {
    pos := 0
    for i := 2; i <= n; i++ {
        pos = (pos + m) % i
    }
    return pos
}