旋转图像

旋转图像

https://leetcode-cn.com/leetbook/read/top-interview-questions-easy/xnhhkv/

https://leetcode-cn.com/problems/rotate-image/

使用临时矩阵

注意到旋转后元素位置和原位置的关系：

  • 原本在第n行，旋转后变成倒数第n列
  • 原本在第m列，旋转后变成第m行

即：matrix[row][col] -> matrix_new[col][n-1-row]

使用一个临时数组，利用上面这个规律更新临时数组。最后再将原数组换成临时数组，达到“原地修改”的目的。

复杂度

时间空间复杂度都是O(n^2)​

实现

1
2
3
4
5
6
7
8
9
10
11
12
void rotate(vector<vector<int>>& matrix) {
    auto temp = matrix;
    int n = matrix.size();

    for (int row = 0; row < n; ++row) {
        for (int col = 0; col < n; ++col) {
            temp[col][n-1-row] = matrix[row][col];
        }
    }

    matrix.swap(temp);
}

原地旋转

直接在原地将每一个元素移动到它应该在的地方，并且把要被覆盖的元素也移动走。容易发现旋转一次，一个位置的元素对应了4个位置的变化，且它们之间组成一个环。因此用temp保存最后一个被覆盖的值，然后依次移动并覆盖即可。

这4个元素旋转一次后，相对于上一个位置的关系都是matrix[row][col] -> matrix_new[col][n-1-row]。转换成相对于第一个位置（绝对位置）的关系：

  1. matrix[row][col] -> matrix_new[col][n-1-row]
  2. matrix[col][n-1-row] -> matrix_new[n-1-row][n-1-col]
  3. matrix[n-1-row][n-1-col] -> matrix_new[n-1-col][row]
  4. matrix[n-1-col][row] -> matrix_new[row][col]

如同上面说的，组成了一个循环。用一个temp变量保 存第一个丢失的值matrix[row][col]即可。

还有一个问题：需要遍历矩阵中的哪些元素？显然，一次这样的操作移动好了4个元素，因此当边长n为偶数时，可以将矩阵分成一样大小的4块，只需操作其中一块；

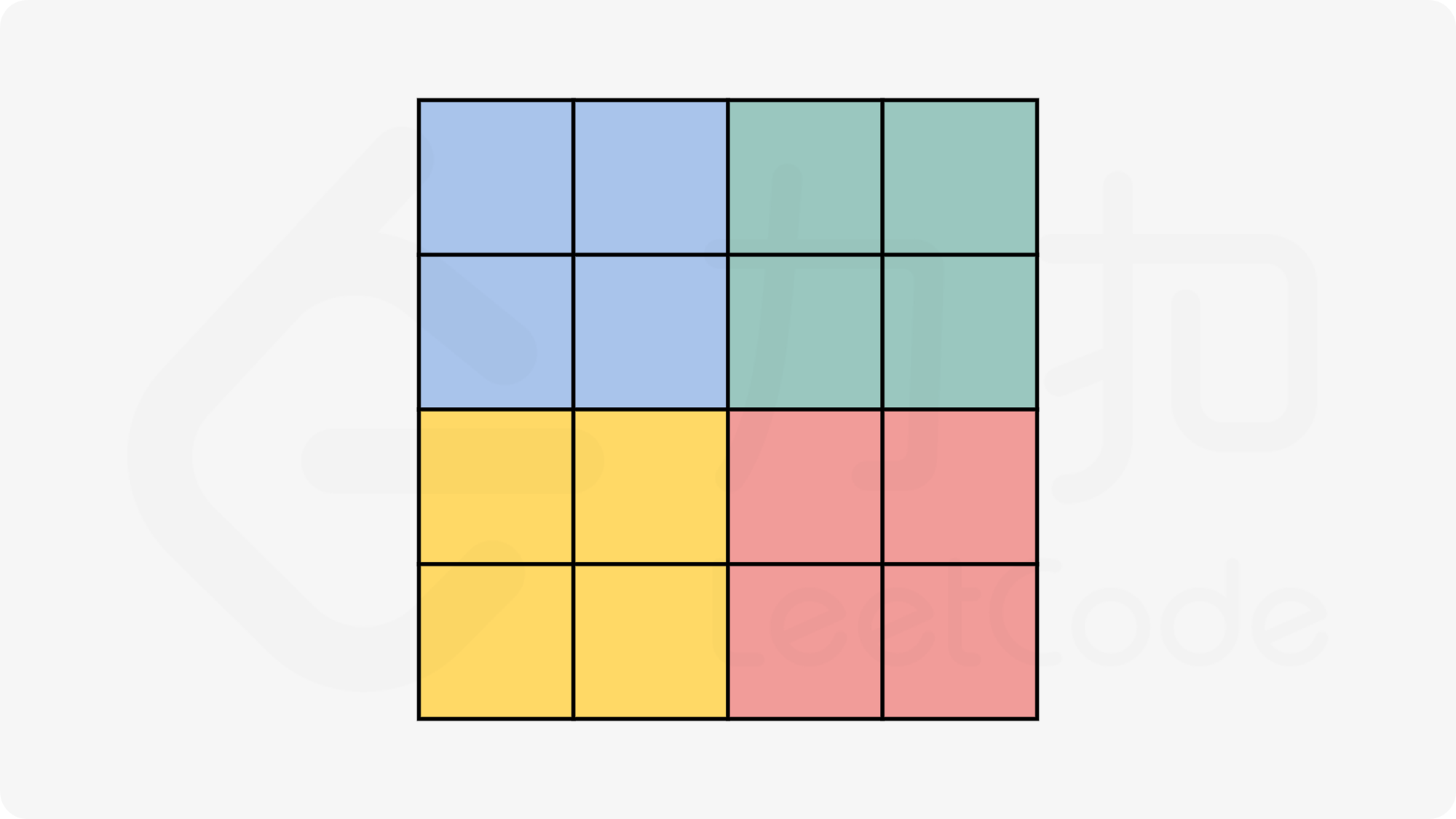
对于左上角的这一块，它的范围是：

  • 行：n/2
  • 列：n/2

如果边长n为奇数的时候呢？使用这种巧妙的方法：

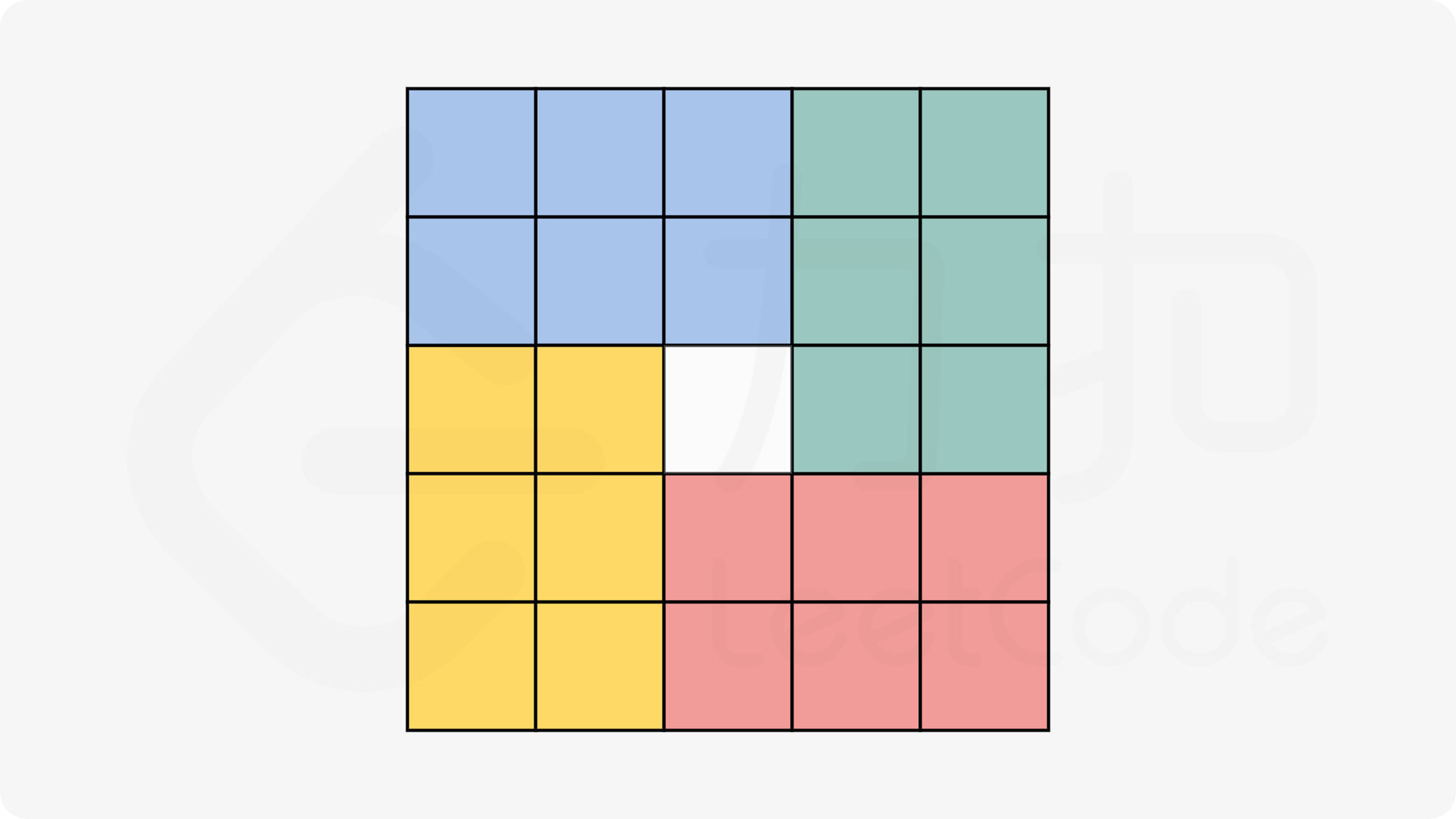
对于左上角这一块，它的范围是：

  • 行：n/2
  • 列：n/2 + 1

综合起来可以写成：

  • 行：n/2
  • 列：n/2 + n%2 （或者(n+1)/2）

复杂度

时间复杂度：O(n^2)

空间复杂度：O(1)

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void rotate(vector<vector<int>>& matrix) {
    int n = matrix.size();
	
    // 注意for循环的范围
    for (int row = 0; row < n/2; ++row) {
        for (int col = 0; col < n/2 + n%2; ++col) {
            int temp = matrix[row][col];
            matrix[row][col] = matrix[n-1-col][row];
            matrix[n-1-col][row] = matrix[n-1-row][n-1-col];
            matrix[n-1-row][n-1-col] = matrix[col][n-1-row];
            matrix[col][n-1-row] = temp;
        }
    }
}

使用翻转来代替旋转

上下翻转，然后主对角线翻转，就能得到答案。

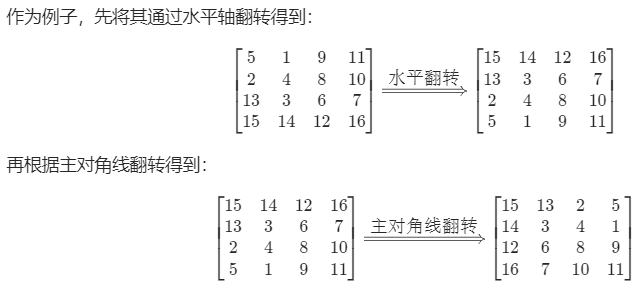
这是根据之前的那个关键公式推断的：matrix[row][col] -> matrix_new[col][n-1-row]。观察这个公式，主要是两点：

  1. row变成了n-1-row（正数变成倒数）
  2. row和col交换（转置）

而1可以用上下翻转得到，这样正数第n行就变成了倒数第n行；2可以通过转置得到，即行号变成列号。

复杂度

时间复杂度：O(n^2)

空间复杂度：O(1)

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void rotate(vector<vector<int>>& matrix) {
    int n = matrix.size();
    // 水平翻转
    for (int i = 0; i < n / 2; ++i) {
        for (int j = 0; j < n; ++j) {
            swap(matrix[i][j], matrix[n - i - 1][j]);
        }
    }
    // 主对角线翻转
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < i; ++j) {
            swap(matrix[i][j], matrix[j][i]);
        }
    }
}